1. 그래프 탐색

V : 정점, E : 간선 ,

- 인접 행렬 : 그래프에서 정점과 간선의 관계, bool 타입의 정사각형 배열, 그래프가 조밀할 때 사용
시간 복잡도 -> O(1) // 간선 1개 ~ O(V²) //모든 간선
공간 복잡도 -> O(V²)
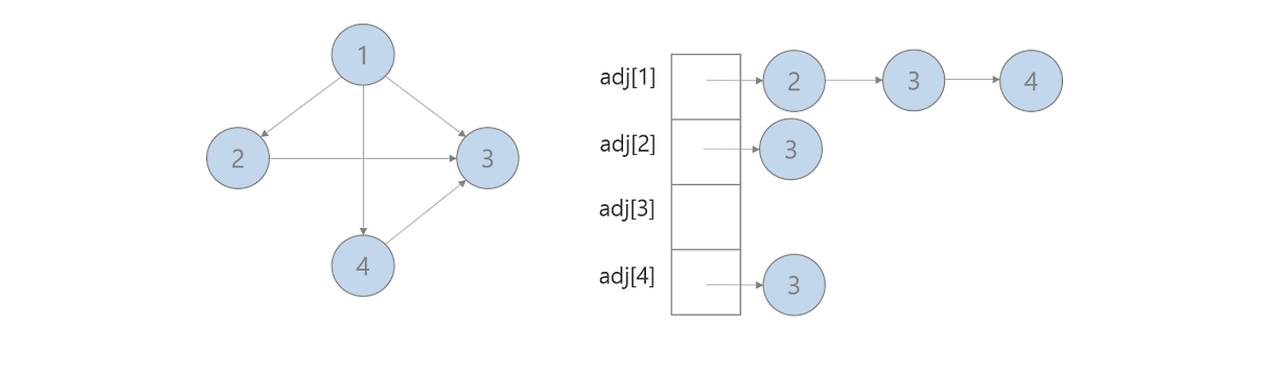
- 인접 리스트 : 정점마다 정점에 대한 연결리스트 작성, 그래프 간선이 희소할 때 사용
시간 복잡도 -> O(V) //1개 ~ O(V+E) // 모든
공간 복잡도 -> O(V+E)
2. DFS, BFS
1) DFS : 다차원 배열에서 각 칸을 방문할 때, 깊이 우선 방문

스택/재귀로 구현, O(N)
장점 : BFS보다 메모리를 덜 씀(현재 경로상 노드만 저장하므로), 코드가 짧음(완전 탐색에 사용)
2) BFS : 다차원 배열에서 각 칸을 방문할 때, 너비 우선 방문

큐로 구현, O(N)
장점 : 최단 거리 구할 때 유용
단점 : 메모리를 DFS보다 더 씀, 코드가 더 길다.
+ 리액트의 diffing알고리즘에서는 BFS를 씀.
DFS로 접근할 경우 변경된 노드에 대해 전체 하위 트리를 리렌더링 하기 때문에 최적화X
동일한 타입의 두 요소를 비교할 때, 기본 노드를 동일하게 유지하고 속성이나 스타일 같은 변경 사항만 업데이트 함.
( * diffing 알고리즘 :새로 생성 된 가상 DOM과 이전 버전과의 차이점을 식별하는 알고리즘)
3. DP

* dp : 하나의 큰 문제를 여러개의 작은 문제로 나누어 해결하고, 그 결과 다시 저장하여 다시 큰 문제 해결 시 사용
* dp 조건
1) 중복되는 부분 문제 : 동일한 작은 문제가 반복적으로 나타날 경우
2) 최적의 부분 구조 : 부분문제 최적의 값이 전체 문제의 최적 결과를 낼 수 있는 경우
* dp 구현 방법
1) bottom - up : 반복문 사용
아래서 계산 후 누적, 전체적인 큰 문제 해결
2) top-down : 재귀 사용
위부터 호출, 결과 값을 재귀 통헤 전이시켜 재활용
'스터디 > CS 스터디 (24.06-24.11)' 카테고리의 다른 글
| 컴퓨터 구조 : CPU 설계 방식(RISC/CISC), 파이프라이닝 (0) | 2024.06.28 |
|---|---|
| 알고리즘 : 시간/공간 복잡도 (0) | 2024.06.28 |
| 컴퓨터 구조 : 컴퓨터의 3대 구성요소, CPU의 동작 원리 (0) | 2024.06.27 |
| 알고리즘 : 정렬(선택, 삽입, 거품, 힙, 병합, 퀵, 팀 정렬) (0) | 2024.06.17 |
| 자료구조 : 트리(편향, 균형, 레드블랙, 다양한 이진트리..) (1) | 2024.06.11 |